Our review article “Numerical approaches on driven elastic interfaces in random media” has been published in Comptes Rendus Physique.
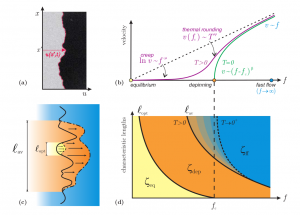
We present the main concepts behind the statistical and dynamical properties of elastic systems in disordered media, focused on the relation between the rough geometry and collective transport properties in driven steady-states. We review the numerical approaches that allow to analyze the equilibrium, creep, and depinning regimes of motion in these models.
We thank Thierry Giamarchi, the Académie des Sciences Guest Editor for this special number, for his vote of confidence.
Ezequiel E. Ferrero, Sebastian Bustingorry, Alejandro B. Kolton, Alberto Rosso
Numerical approaches on driven elastic interfaces in random media
Comptes Rendus Physique, Volume 14, Issue 8, October 2013, Pages 641–650
http://dx.doi.org/10.1016/j.crhy.2013.08.002